This document provides the mathematical and geophysical foundations behind SubsurfaceAI’s AVO calculation using partial stacks. It elaborates the equations and assumptions behind estimating intercept and gradient from angle/offset-limited stacks, demonstrates the workflow with numerical examples, and discusses stability conditions and model limitations.
1. The Zoeppritz Equations and Linear Approximations
1.1 Exact PP Zoeppritz Reflection Coefficient
The exact PP reflection coefficient for an incident P-wave at an interface is given by the Zoeppritz equations:
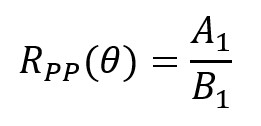
where A1 and B1 depend on1:
- P-wave velocities VP1, VP2
- S-wave velocities VS1, VS2
- Densities P1, P2
- Incident angle θ
In practice, Zoeppritz equations are rarely used directly for AVO interpretation due to their complexity and sensitivity to noise.
1.2 Aki–Richards Approximation (3-Term)
The most commonly applied practical approximation for AVO analysis is the Aki–Richards equation:
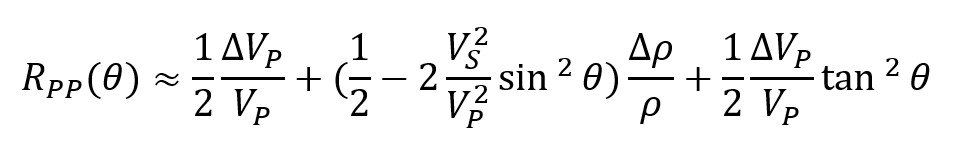
Where:
For moderate angles (≤ 30°), this approximation is sufficiently accurate for most seismic datasets.
1.3 Shuey (2-Term) Approximation
SubsurfaceAI’s intercept (A) and gradient (B) derive from the two-term Shuey form:
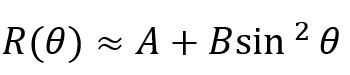
Where: 
Interpretation geophysicists can understand:
- A acts like zero-angle reflectivity
- B accounts for Poisson’s ratio (fluid sensitivity)
- Gas sands often show negative A and strong negative B
This simplified model forms the basis for partial-stack AVO attribute calculation.
2. AVO from Partial Stacks: Mathematical Formulation
Assume we have K partial stacks, each representing a narrow angle band:
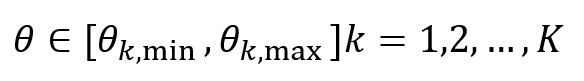
SubsurfaceAI requires user-defined angle ranges per stack.
2.1 Effective Angle per Partial Stack
A partial stack represents a set of angles averaged over many traces. The effective angle for stack k is:
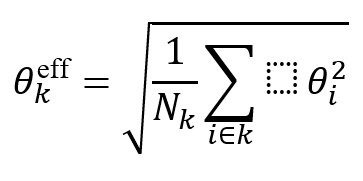
or simply the center angle:
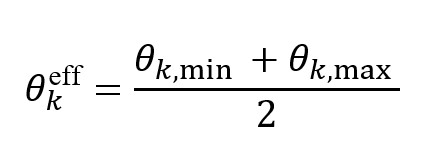
SubsurfaceAI allows users to provide stack angle ranges; effective angles are computed automatically.
2.2 Linear AVO Model for Partial Stacks
If dk is amplitude in partial stack k:

where ϵk captures noise and stack averaging error.
For all stacks:
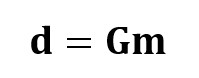
where:

and:

2.3 Solving for Intercept and Gradient (Least Squares)
If K ≥ 2, the least-squares estimate is:
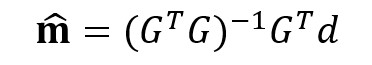
Explicitly:
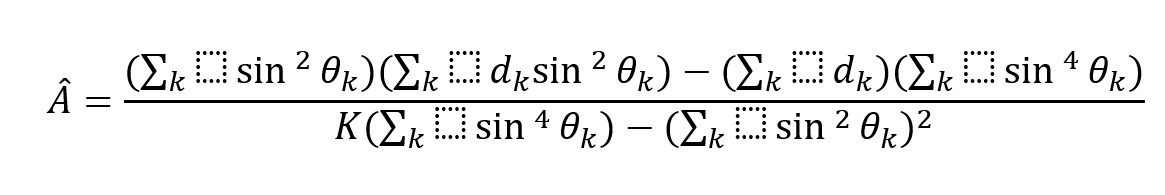
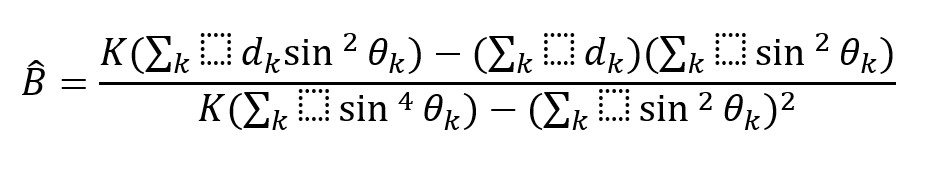
These equations are implemented internally in SubsurfaceAI.
2.4 Special Case: Two Partial Stacks
For near and far stacks only:
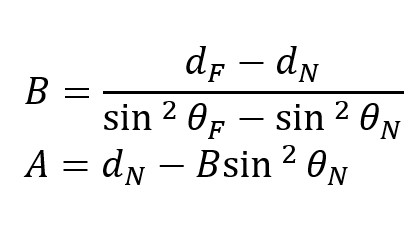
This provides stable AVO when only 2 stacks are available (the most common industry case).
3. Worked Numerical Examples
Below are several numerical AVO examples suitable for checking partial-stack behavior.
3.1 Example 1 – 2 Partial Stacks (Near/Far)
Given:
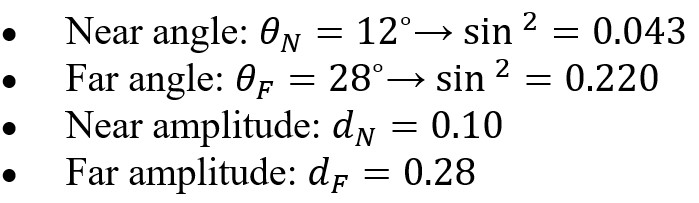
Gradient:

Intercept:
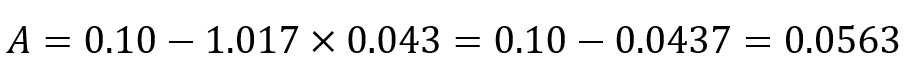
This (A,B) = (0.056,1.02) pair plots in the positive intercept, strong positive gradient region.
3.2 Example 2 – 3 Partial Stacks (More Stable Estimate)
Given:

The least-squares results:
![]()
Interpretation:
- Still Class III-like (increasing amplitude vs angle)
- Higher robustness because of the mid-angle stack
- Far stack amplitude strongly influences slope
3.3 Example 3 – Effect of Angle Misassignment
Suppose actual mid angle is 20°, but user accidentally enters 10–15° range (effective angle → 12.5°).
This compresses sin2 θ, yielding artificially large B values.
Quantitatively:
- True slope ~1.07
- Misassigned slope ~1.31
Interpretation:
Accurate angle range input is essential; SubsurfaceAI’s UI emphasizes angle validation for this reason.
4. Error and Stability Analysis
4.1 Condition Number of G
The stability of AVO inversion depends on: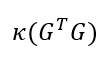
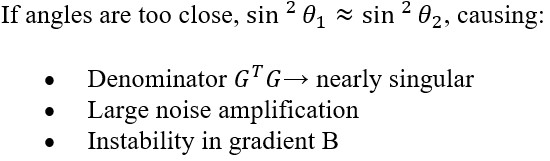
Practical guidance (SubsurfaceAI constraint):
- Use angle ranges spanning at least 10–15 degrees difference
- Prefer 3 or more partial stacks if available
4.2 Noise Propagation
Model:
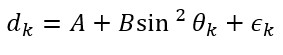
Variance of estimated B:

Hence:
- Higher angle spread → lower B uncertainty
- Far-angle noise has largest influence on B
4.3 Partial Stack Averaging Errors
Because each stack represents a band of angles:
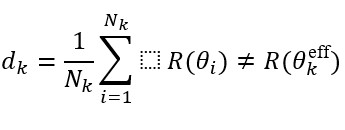
Taylor expansion shows:
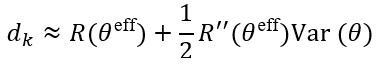
Thus:
- Wide angle bands introduce second-order error
- Narrower stacks yield more accurate AVO
- SubsurfaceAI allows up to 5 stacks to minimize bandwidth per stack
5. AVO Beyond Intercept and Gradient: Higher-Order Effects
While SubsurfaceAI’s workflow is optimized for A–B analysis using partial stacks, more advanced AVO components are worth noting.
5.1 Shuey 3-Term Approximation
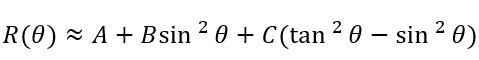
where C is the curvature term.
Curvature requires:
- At least 4–5 distinct angles
- Smaller angle increment
- Far angles up to 35–40°
SubsurfaceAI can compute curvature if the user provides 4–5 stacks, but the workflow retains an interpreter focus and primarily uses two-term AVO.
5.2 Ruger’s Azimuthal AVO (AVAz)
AVAz requires:
- Full azimuthal angle coverage
- Gather-based pre-stack data
Partial stacks generally do not preserve azimuthal variation unless specifically processed in azimuthal bins.
SubsurfaceAI does not compute AVAz from partial stacks.
6. Fluid Stack and Lithology Stack: Mathematical Projection Methods
Fluid stack and lithology stack attributes are directional projections in A–B space.
Let:
![]()
Define fluid direction vector uf :
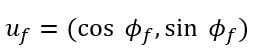
and lithology direction vector uf:
![]()
Then:
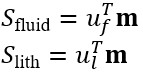
These formulas generate continuous properties that SubsurfaceAI displays directly as seismic volumes.
7. Synthetic Rock-Physics-Based Examples
Below are several rock-physics scenarios mapped into AVO intercept and gradient.
Example 1 – Gas Sand in Shale
Elastic contrast:
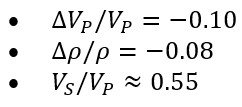
Shuey:
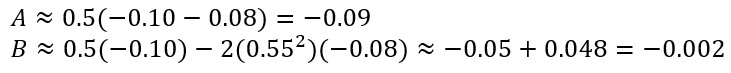
Gas sands often have negative intercept, but gradient depends strongly on Vp/Vs contrast.
Example 2 – Brine Sand in Shale
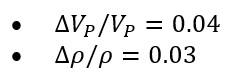

Brine sands → positive intercept, near-zero gradient.
Example 3 – Hard Carbonate Over Soft Shale
- High positive impedance contrast
- Strong positive A
- Moderate negative B
These clusters appear clearly in SubsurfaceAI cross-plots.
8. Practical Gain: How Partial-Stack AVO Supports Interpretation in SubsurfaceAI
The mathematical rigor above is embedded completely inside SubsurfaceAI’s intuitive interface. The interpreter:
- selects partial stacks,
- enters angle ranges,
- runs AVO,
- interprets AVO classes,
- defines fluid/lithology directions,
- extracts geobodies, and
- resamples results to reservoir grids.
No coding. No math manually performed.
9. Final Summary of Technical Insights
- SubsurfaceAI uses a least-squares inversion of partial stack amplitudes to compute intercept and gradient.
- Users provide angle ranges; SubsurfaceAI computes effective angles.
- Up to 5 partial stacks→ robust estimation of A, B, and even curvature terms if desired.
- Stability depends on angle spacing and stack bandwidth.
- Partial-stack AVO is not equivalent to gather-based inversion, but is highly effective for interpretation-scale workflows.
- Fluid and lithology stacks arise from directional projections in A–B space.
- Facies and property volumes derived from AVO can be resampled to static reservoir grids for model integration.
